matlab - coded filter vs fdatool : inconsistency in the results for same parameters

I tried creating a filter in 2 different ways in Matlab and I obtain different results: one filter is stable, whereas the other one is unstable.

Coded filter

delta_t = 1.53846e-04;
Fs = 1/delta_t;


cut_F = 8; 
Wn = cut_F/(Fs/2);
ftype = 'high';
[b,a] = butter(8,Wn,ftype);
fvtool(b,a)

The result is an unstable filter

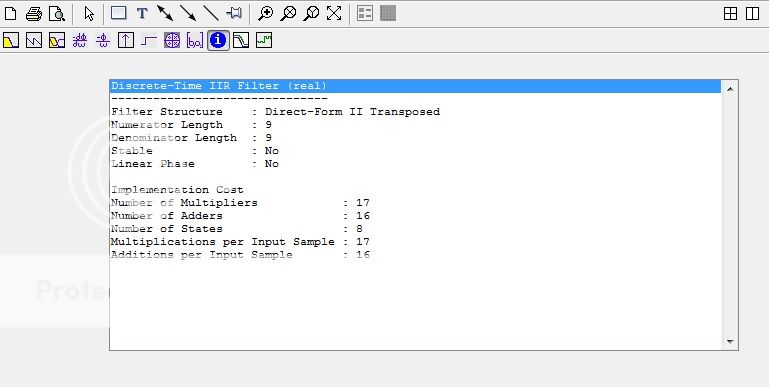
fdatool

This is what I obtain with the toolbox using the same parameters:

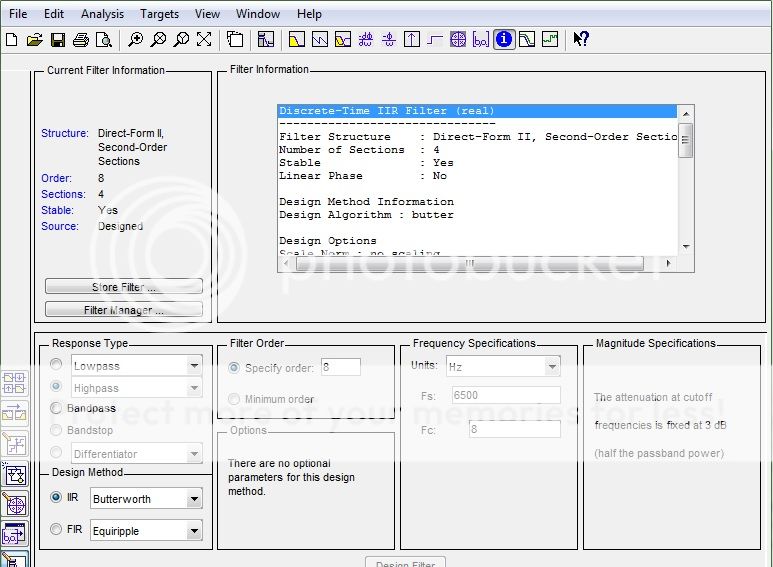
I am using already implemented functions in both cases...Why I get so different results?

Answer

Note that the fdatool gives you a structure with cascaded second-order sections, whereas the fvtool uses a direct-form II transposed structure. In combination with the filter specs this results in the difference you see, because the very low cut-off frequency combined with the relatively high filter order results in a cluster of poles and zeros very close to the DC point in the complex $z$-plane (i.e., close to $z=1$). Computing the exact locations of the poles and zeros is an ill-conditioned problem, and in the case of the direct-form II transposed structure, you need to find the roots of polynomials of degree $8$. Due to the round-off errors in the computation of the roots, some of the poles appear to lie just outside the unit circle, hence the conclusion that the filter is unstable. For the second order sections, the poles can be computed more accurately and they all turn out to lie inside the unit circle, hence the conclusion that the filter is stable.

So, is the filter now stable or unstable? Well, in theory it is stable. In practice, however, it is probably of no use because its poles are virtually on the unit circle. The tool probably offers you to compute the exact pole locations of the second order sections. You'll see that most of the pole radii are very close to $1$.