Hilbert transform filter for audio applications: Using IIR half-band parallel all pass structure

Does anyone have any experience designing wideband IIR Hilbert transform filters with audio applications in mind? I am using the filter for single side band modulation audio effects discussed in this paper :-http://www.mikrocontroller.net/attachment/33905/Audio_Hilbert_WAR19.pdf.

I tried to implement the design technique discussed in this paper:- http://www.aes.org/e-lib/browse.cfm?elib=15680 but have not been able to achieve the results in the paper using frequency warping.

Any help on the topic is appreciated; please find MATLAB code below.

Update: I now achieve better results without warping with some loss in accuracy in the magnitude response.

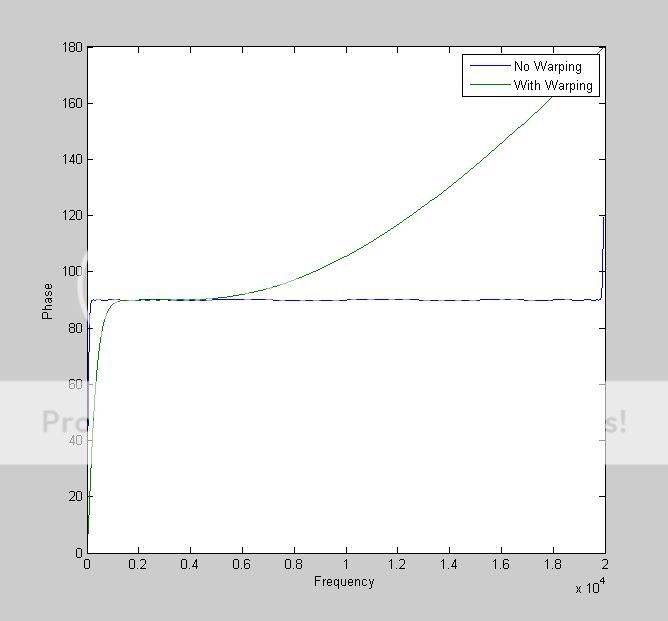
Frequency Warping:

Half band frequencies:-

$\omega _{p}= \tan^{-1}\left [ \left ( \frac{\tan \frac{\omega _{1}}{2}}{\tan \frac{\omega _{2}}{2}} \right )^{\frac{1}{2}} \right ]$

$\omega _{s}= \tan^{-1}\left [ \left ( \frac{\tan \frac{\omega _{2}}{2}}{\tan \frac{\omega _{1}}{2}} \right )^{\frac{1}{2}} \right ]$

$ \text{Where } \omega _{1} \text{ and }\omega _{2} \text{ is the hilbert frequency range}$

Warping:-

$z^{-1}= \frac{k_{b}+z^{-1}}{1+k_{b}z^{-1}}$

$k_{b} = \frac{\beta -1}{\beta +1}$

$\beta = \left [ \tan \frac{\omega _{1}}{2}\tan \frac{\omega _{2}}{2} \right ]^{_{\frac{1}{2}}}$

$c_{new} = \frac{-p+k_{b}}{1-pk_{b}} $

$ \text{Where } c_{new} \text{ is the new filter coefficient and } p \text{ is the filter pole} $

Code

%% IIR Hilbert transformer pair
%specifacation
fs = 40000;
fsinv = 1/fs;
w1 = 200*fsinv*pi*2;
w2 = fsinv*15000*pi*2;


% prewarp spec
wp_hil = 2*atan(sqrt((tan(w1/2))/(tan(w2/2))))
ws_hil = 2*atan(sqrt((tan(w2/2))/(tan(w1/2))))

% halfband spec
%wp = (pi/2)-wp_hil; 
A_s = 80;

% Calculate poles for A0(z) and A1(z)

[alpha_dash] = IIR_Halfband(wp_hil ,ws_hil ,A_s); 

% Calculate poles for A0(z^2) and A1(z^2)
alpha = sort([1j*sqrt(alpha_dash) -1j*sqrt(alpha_dash)]);

% Convert to hilbert transform filter & interlace poles
var = 0;
idx_a = 1;
idx_b = 1;
A1_p = zeros((length(alpha))/2,1);

A0_p = zeros((length(alpha))/2,1);
for idx = length(alpha):-1:1
    if (var <2)
        A1_p(idx_b) = 1j*alpha(idx);
        var = var + 1;
        idx_b = idx_b +1;
    else
        A0_p(idx_a) = 1j*alpha(idx);
        var = var + 1;
        idx_a = idx_a +1;

        var = mod(var,4);
    end
end
A1_p = [0;A1_p]; % additional delay element for imajinary path

% Frequency warping
A1_p2 = zeros((length(A1_p)),1);
A0_p2 = zeros((length(A0_p)),1);

beta = sqrt((tan(w1/2))*(tan(w2/2)));

kb = (beta-1)/(beta+1);
for idx = 1:length(A1_p2)
    A1_p2(idx) = (-A1_p(idx)+ kb)/(-A1_p(idx)*kb +1);
end
for idx = 1:length(A0_p2)
    A0_p2(idx) = (-A0_p(idx)+ kb)/(-A0_p(idx)*kb +1);
end

% generate transfer functions
sys_i = tf([A1_p2(1) 1],[1 A1_p2(1)],fs,'Variable','z^-1');

sys_r =1;
for idx = 1:length(A0_p)
    sys_i = sys_i*tf([A1_p2(idx+1) 1],[1 A1_p2(idx+1)],fs,'Variable','z^-1');
    sys_r = sys_r*tf([A0_p2(idx) 1],[1 A0_p2(idx)],fs,'Variable','z^-1');
end

% plot filter atributes
%fvtool(cell2mat(sys_r.num),cell2mat(sys_r.den))
%fvtool(cell2mat(sys_i.num),cell2mat(sys_i.den))


% phase difference
[phi,w] = phasez(cell2mat(sys_r.num),cell2mat(sys_r.den)) ;
[phi2,w] = phasez(cell2mat(sys_i.num),cell2mat(sys_i.den)) ;
plot(w/(2*pi),180*((phi-phi2)/pi))

Half-band filter design function based on Program 13_9 in Digital Signal Processing: A Computer-Based Approach 3ed http://highered.mcgraw-hill.com/sites/0072865466/

% IIR Lowpass Half-band Filter Design
function[alpha] = IIR_Halfband(wp,ws,A_s) 
% Enter filter stopband specifications


%ws = pi - wp;
delta_s = 10^(-(A_s/20));
% Order estimation
r = tan(0.5*wp)/tan(0.5*ws);
r_hat = sqrt(1-(r^2));
q0 = 0.5*(1-sqrt(r_hat))/(1+sqrt(r_hat));
q = q0+2*(q0^5)+15*(q0^9)+150*(q0^13);
D = ((1-(delta_s^2))/(delta_s^2))^2;
N = ceil((log10(16*D))/(log10(1/q)))
if (mod(N,2) == 0)

    N = N+1
end;
% Readjusting ripple size
D = (1/16)*(10^(N*log10(1/q)));
delta_s = sqrt(1/(1+sqrt(D)));
% Computing filter coefficients
alpha = zeros(length((N-1)/2),1);
for k = 1:(N-1)/2,
    sum1 = 0;sum2 = 0;
    for i = 0:6,

        sum1 = sum1+((-1)^i)*(q^(i*(i+1)))*sin((2*i+1)*k*pi/N);
        if (i ~= 0)
        sum2 = sum2+((-1)^i)*(q^(i^2))*cos(2*pi*k*i/N);
        end;
    end;
    lambda(k) = (2*q^(0.25)*sum1)/(1+2*sum2);
    b(k) = sqrt((1-r*(lambda(k)^2))*(1-(lambda(k)^2)/r));
    c(k) = (2*b(k))/(1+(lambda(k)^2));
    alpha(k) = (2-c(k))/(2+c(k));
end;

alpha = sort(alpha);
end